Tower of Hanoi Program

Python Program – Tower of Hanoi

The Tower of Hanoi is a classic puzzle game consisting of three pegs and a number of disks of different sizes, which can slide onto any peg.

The puzzle starts with the disks in a neat stack in ascending order of size on one peg, the smallest at the top, thus making a conical shape. The objective of the puzzle is to move the entire stack to another peg.

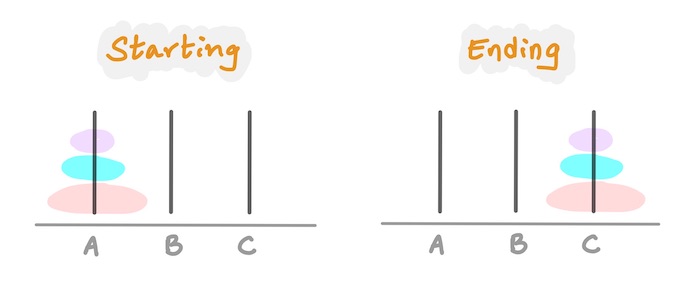
And the movement of disks between the pegs must obey the following simple rules:

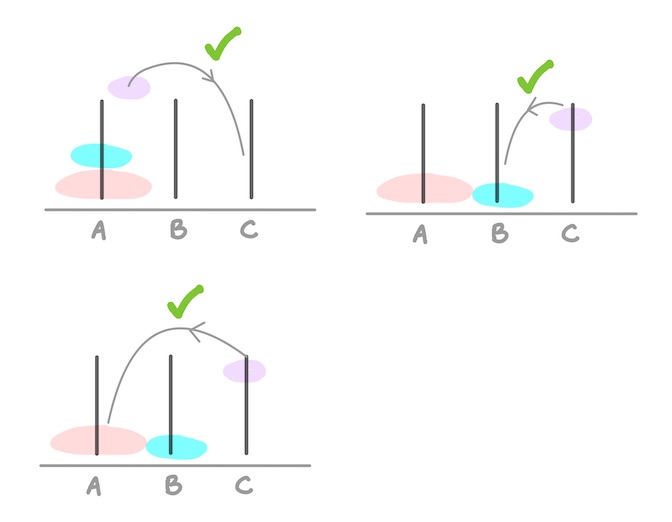
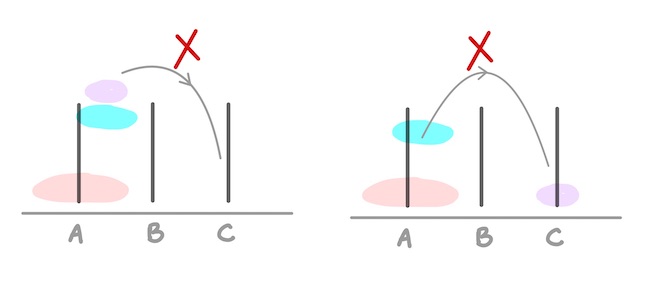
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty peg.
3. No disk may be placed on top of a smaller disk.

The puzzle is commonly used in computer science and programming as an example of a recursive function.

Tower of Hanoi Program using Recursion

In the following program, we will use recursion technique to solve the Tower of Hanoi problem.

tower_of_hanoi() function has four parameters.

1. n – the number of disks.
2. from_rod – The rod which has all the disks at the start.
3. to_rod – The rod to which all the disks has to be moved.
4. aux_rod – The auxiliary rod which can be used to place the disks temporarily.

def tower_of_hanoi(n, from_rod, to_rod, aux_rod):
    if n == 1:
        print("Move disk 1 from rod", from_rod, "to rod", to_rod)
        return
    tower_of_hanoi(n-1, from_rod, aux_rod, to_rod)
    print("Move disk", n, "from rod", from_rod, "to rod", to_rod)
    tower_of_hanoi(n-1, aux_rod, to_rod, from_rod)
 
# Number of disks
n = 4
tower_of_hanoi(n, 'A', 'C', 'B')

Output

Move disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C

Summary

In this tutorial, we learned how to solve the problem of Tower of Hanoi using recursion, with examples.